General Trees & Binary Trees

CSC Data Structures and Algorithms

Brian-Thomas Rogers

broge2@uis.edu

University of Illinois Springfield

College of Health, Science, and Technology

Contents

• Objectives
• Tree Basics
• Tree Applications
• Tree Traversals
• Binary Tree Implementation
• Removing a Node
• Traversal Algorithms
• Finished

Objectives

Objectives

• Become familiar with the basic terminology used to describe trees
• Know how trees can be described recursively
• Understand the four major traversals of trees
• Know the difference between breadth-frist versus depth-first traversal
• Become familiar with the basics of binary tree implementation

Tree Basics

Tree Basics

• Trees provide a hierarchical organization of data
  • Data items have ancestors and descendants
  • Data items appear at various levels
• A tree consists of a set of linked nodes each of which may have links to one or more child nodes
• Child nodes do not typically have links to their parent nodes
• One node is typically designated the root node where the tree starts and all other nodes are descendants of the root node
  • The root is the ancestor to all other nodes
• A binary tree is a special type of tree which limits the number of child nodes to at most 2.

Tree Terminology

Visual representation of various tree terms

Tree Terminology Cont.

• Leaves: Nodes with no children.
• Subtree: A given node in the tree and its descendants.
• Every node in the tree has the following implicit attributes
  • Depth (also called level): The length of the path from the root node to the node
    • In the previous slide, Node I has depth 2.
  • Height: The length of the path from a node to its deepest leaf
    • Node I in the previous slide has height 1
    • The height of a tree is the height of its root
  • Size: The total number of descendants the node has plus itself

Tree Terminology Cont.

• The next set of terminology is specific to Binary Trees
• Full Binary Tree: A binary tree in which all nodes, except the leaf nodes, have exactly two children
• Complete Binary Tree: A binary tree in which every level, except possibly the last level, contains the maximum number of nodes and nodes in the last level are filled from left to right
• Perfect Binary Tree: A binary tree in which all interior nodes have two children and all leaves have the same depth. Perfect binary trees are full and complete binary trees.

Full vs. Complete

Examples of full vs complete

Note

Tree a shows a perfect binary tree. It is not necessarily true that a tree that is full is also complete and vice versa. Tree b is complete but not full. Node L only has 1 child which violates the “exactly 2 child nodes” of a full tree.

Number of Nodes and Height

• There is a relationship between the number of nodes and the tree height of a perfect binary tree

Perfect binary trees and their relationships

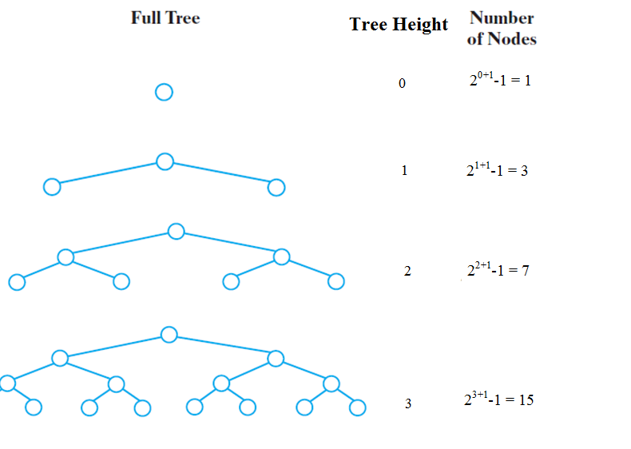
\[ n = 2^{h + 1} - 1 \]

• \(n\) is the number of nodes
• \(h\) is the height
• Number of leaf nodes (\(l\)) can be calculated

\[ l = 2^h \]

Definition Differences

• The book uses a different definition of height and depth
• In the book, the height of a one node tree has height one
• We use the definition of the height of a one node tree to be zero
• Use the definition provided in these slides for quizzes and exams

Tree Applications

Tree Applications

• The use of trees in computer science is vast
• Trees are not just a collection but are used to model problems
• Some applications include
  • Decision Trees
  • Expression Trees
  • Game Trees
  • HTML/XML
  • File systems
  • Compression Algorithms
  • Cryptography
  • and many many more…

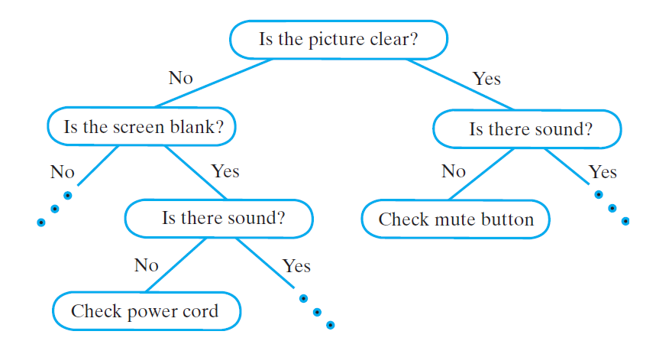
Example of Decision Trees

• Expert systems use decision trees to provide solutions based on inputs
  • Helps users solve problems
  • Parent node asks a question
  • Child nodes provide conclusion or further questions

Decision tree for a help desk system

Example of Expression Trees

• Trees are used widely in compilers to represent the structure of a program

Examples of expression trees

Example of Game Trees

• The goal of game trees is used in game playing AI as an attempt to find the best move to make

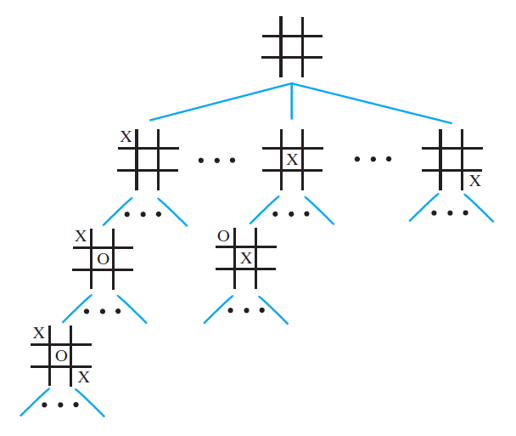
Game Tree for Tic Tac Toe

Tree Traversals

Tree Traversals

• Must process each node exactly once
• Nodes can be visited in different orders
• For a binary tree
  • Visit the root
  • Visit all nodes in root’s left subtree
  • Visit all nodes in root’s right subtree
• A binary tree can be traversed in three different ways depending on whether the parent node is processed before, between, or after the subtrees

Pre-Order Traversal

• The order of processing nodes
  • Parent then left subtree then right subtree

The order in which each node is processed in pre-order

In-Order Traversal

• The order of processing nodes
  • Left subtree then parent then right subtree

The order in which each node is processed in in-order

Post-Order Traversal

• The order of processing nodes
  • Left subtree then right subtree then parent

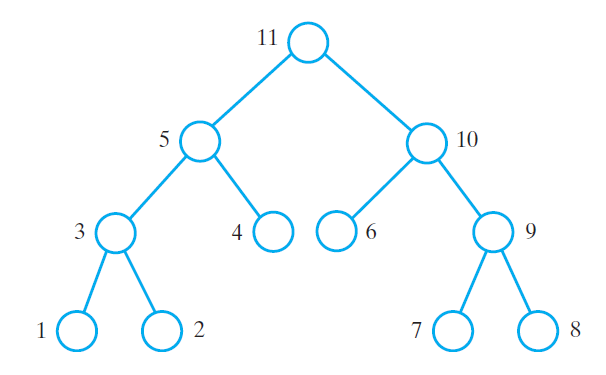
The order in which each node is processed in post-order

Example Traversal of Expression Tree

• Suppose the compiler built the following tree for the expression \(2 * (4 - (5 + 3))\)

• Pre-Order Traversal
  • \(* \ 2 - 4 + 5 \ 3\)
• In-Order Traversal
  • \(2 * 4 - 5 + 3\)
• Post-Order Traversal
  • \(2 \ 4 \ 5 \ 3 + - *\)

Depth-First Traversal

• The traversals we looked at are all depth-first traversals
  • Depth-first traversal seeks to traverse as deep as possible in one direction and when it can go no deeper it backtracks to the next available path it has not yet visited.

Breadth-First Traversal

• Breadth-First traversal is the opposite of depth-first
• It visits all nodes in one level before going to a deeper level
  • Top-to-bottom, left-to-right
• It is also called level-order traversal

The order in which each node is processed in level-order

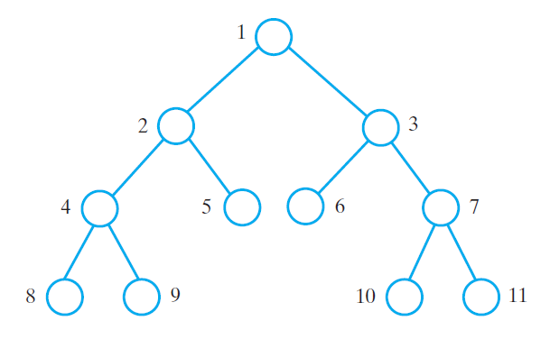
Use of Breadth-First vs. Depth-First

• Breadth-first traversal can be used for finding the shortest path between two nodes in a graph
• A depth-first traversal might be used to determine whether a path exists between two nodes in a graph
• Both of these traversals (also known as searches) are building blocks for many advanced algorithms including
  • AI
  • Routing in Computer Networks
  • Compiler Optimizations

Note

Graphs are the general data structure of connected nodes (or vertices) via edges created by one Leonhard Euler in 1735. The field of studying graphs is known as graph theory. Trees and linked lists are special types of graphs.

Implementing Breadth-First vs. Depth-First

• Depth-first traversals on trees are easily implemented with recursion
  • This means they can be implemeneted with Stacks as well
• Breadth-first traversals on trees is not as easily implemented recursively, nor is it very efficient
  • Breadth-first prefers to be implemented with a Queue data structure

Binary Tree Implementation

Quick Thoughts

• The following is an implementation of a Binary Tree as general storage like a List
• My opinion on this is that it is not a good idea to use a Binary Tree on its own as just a storage mechanism
• If storage is all that is needed then use a List structure
• If, however, the data has some form of hierarchy that must be maintained then a tree structure is preferred
• The following should be used to understand how trees can be formed but more importantly how to do the traversals on a tree

Binary Tree Implementation

• Inner Class BinaryNode
  • Attributes
    • data: stores the data item in the node
    • leftChild: a reference to the left child
    • rightChild: a reference to the right child
  • Two Constructors
    • One that takes just a data item and creates a new binary node with no children
    • One that takes a data item as well as a left and right child node

Height Methods

• getHeight(BinaryNode node)
  • A private utility method
  • Returns the height of a given node in the tree
  • The height is computed recursively by using the following rule
    • Height of a node is equal to the height of the max of left or right subtree plus 1
    • Stopping criteria is when we reach a null node which returns -1
    • Has \(O(n)\) runtime
• height()
  • Public method that returns the height of the entire tree by calling height(root)

Retrieval

• getRootItem: Returns item in root or throws an exception if tree is empty
• get: Simply calls getRootItem
• getNode(T obj): Private utility method that returns the BinaryNode object which contains obj. Returns null if the obj does not exist.
• getParentNode(BinaryNode node): Private utility method that returns the parent node of node. If node == root then null is returned.

Adding

• add(T obj)
  • Adds a given item to the tree but where in the tree?
  • An item will always be added at the first available position as determined by level-order traversal of the tree keeping the tree as complete as possible
  • If an item can be add as either left or right child the item is added as the left child by convention
  • Has \(O(n)\) runtime.

Example of Adding

Example of adding to a Binary Tree

Removing

• remove()
  • Up to the programmer which node to remove
  • Standard is to remove the root node
• remove(T obj)
  • Removes a specific item from the tree
  • Use getNode(T obj) to retrieve the BinaryNode object of obj.
  • If the node exists then call remove(node) to remove the node object
  • If the node does not exist then throw an exception

Important

We will discuss the algorithm for removing later using two different methods

Searching

• contains(T obj)
  • Call getNode(T obj)
  • If a node is returned by getNode then return true
  • If null is returned by getNode then return false

Removing a Node

• When we remove a node we must keep maintain the complete tree structure
• This done with a simple algorithm
  • If the node is the root node and is the only node in the tree simply call clear, otherwise…
  • Find the node that contains the object we want to remove
  • Find the last node of the tree
  • Replace the data in the node with the data in the last node in the tree
  • Find the parent of the last node of the tree
  • Remove the last node using the parent which is always a leaf node

Example of Removing a Node

• Suppose we want to remove B from the following tree

Initial Tree

Replace “B” with “F”

Example of Removing a Node Cont.

Result of replacing B with last node

Remove the last node of the tree using the parent

Removing a Node

• The algorithm preserves the complete binary tree structure
• Requires traversing the tree 3 times
  • Once to find the object
  • Once to find the last node of the tree
  • Once to find the parent of the last node of the tree
• The process is still \(O(n)\)

Alternative Remove Algorithm

• If maintaining the complete binary tree structure is not important then you have another choice for an algorithm
  • Shift the item in the node’s left child up one level to replace the item we are removing
  • Continue this process for the left child until you reach a node that does not have a left child and retrieve the parent of this current node
  • You now have 3 cases to consider
    • The node being removed is the root node
      • Replace the root node to the current node’s right child
    • The node being removed is the parent’s left child
      • Set parent’s left child to node’s right child
    • The node being removed is the parent’s right child
      • Set the parent’s right child to the node’s right child

Alternative Remove Example 1

First, shift

Second, remove

Alternative Remove Example 2

Removing Node C

• C does not have any left children so no shifting is done
• We want to remove C and since it is the right child we replace the parent’s right child with C’s right child

Traversal Algorithms

Traversal Algorithm

• We will take a look at the traversal algorithms
• We will look at level-order traversal as it is applied with queues
• We will look at the depth-first traversals as they are applied with recursion and with stacks

Level-Order Traversal

• Level order traversal is performed with a queue
• The queue should be initialized with the root node
• While the queue is not empty
  • Dequeue the front node and process it
  • Add the left and right child nodes of node if they exist to the queue

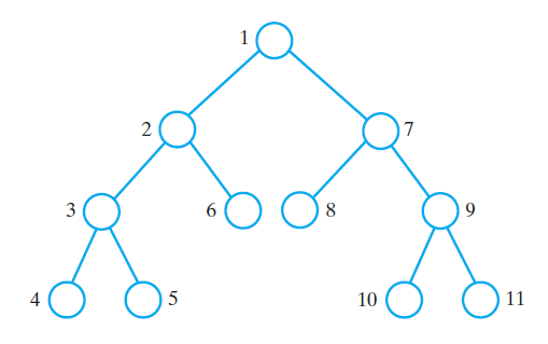
Level-Order Traversal Example

queue [a] -> Root

queue [b c] -> Add children of a

queue [c d e] -> Add children of b

queue [d e f] -> Add children of c

queue [e f] -> d has no children to add

queue [f] -> e has no children to add

queue [g] -> Add children of f

queue [] -> g has no children to add

Done

Recursive Pre-Order Traversal

• The way the pre-order traversal is defined is how the recursive algorithm works
• You first process the parent node then traverse the left subtree then the right subtree.
• Pseudocode

algorithm pre-order() {
  pre-order(root)
}

algorithm pre-order(Node node) {
  if node is not null {
    process(node)
    pre-order(node.leftChild)
    pre-order(node.rightChild)
  }
}

Pre-Order With a Stack

• Using a stack to perform pre-order works like the following
• Initialize stack with root node
• While stack is not empty
  • pop and process top of stack
  • push right child onto stack
  • push left child onto stack

Pre-Order With Stack Example

stack [a] -> Root

stack [c b] -> Add children of a

stack [c e d] -> Add children of b

stack [c e] -> d has no children

stack [c] -> e has no children

stack [f] -> Add children of c

stack [g] -> Add children of f

stack [] -> g has no children

Done

Recursive Post-Order

• The way the post-order traversal is defined is how the recursive algorithm works
• You process left subtree then right subtree then parent
• Pseudocode

algorithm post-order() {
  post-order(root)
}

algorithm post-order(Node node) {
  if node is not null {
    post-order(node.leftChild)
    post-order(node.rightChild)
    process(node)
  }
}

Post-Order With a Stack

• With post-order it is not just about changing where the node is processed from pre-order when using a stack
• Initialize stack with root
• While stack is not empty
  • pop the next node from the stack
  • if this is the first time this node has been popped then we have not visited its left child so push the node back to the stack followed by its left child
  • if this is the second time the node has been popped then we have not visited its right child so push it back on the stack as well as its right child
  • if this is the third time the node has been popped then the node is ready to be processed

Post-Order With Stack Example

stack [a] -> Push root onto stack

• First visit to a

stack [a b]

• First visit to b

stack [a b d]

• First visit to d (Stack remains the same)
• Second visit to d (Stack remains the same)
• Third visit to d can now be processed

stack [a b]

Post-Order With a Stack Cont.

…

• Second visit to b

stack [a b e]

• First visit to e
• Has no children so can be processed

stack [a b]

• Third visit to b can now be processed

stack [a]

Post-Order With a Stack Cont.

…

• Second visit to a

stack [a c]

• First visit to c

stack [a c f]

• First visit to f (Stack remains the same)
• Second visit to f

stack [a c f g]

Post-Order With a Stack Cont.

…

• First visit to g (Stack remains the same)
• Second visit to g (Stack remains the same)
• Third visit to g can now be processed

stack [a c f]

• Third visit to f can now be processed

stack [a c]

Post-Order With a Stack Cont.

…

• Third visit to c can now be processed

stack [a]

• Third visit to a can now be processed

stack []

Done

Recursive In-Order

• The way the in-order traversal is defined is how the recursive algorithm works
• You process left subtree then parent then right subtree
• Pseudocode

algorithm in-order() {
  in-order(root)
}

algorithm in-order(Node node) {
  if node is not null {
    in-order(node.leftChild)
    process(node)
    in-order(node.rightChild)
  }
}

In-Order With a Stack

• Procedure is similar to that of post-order with one difference
• If a noded is popped for the second time you process it and push the right child without putting it back on the stack
• The process looks similar to that of Post-Order with a stack minus the node needing to be visited a third time before being processed

Finished

postorder(root)