Recursion

CSC 385 - Data Structures and Algorithms

Brian-Thomas Rogers

broge2@uis.edu

University of Illinois Springfield

College of Health, Science, and Technology

What is Recursion?

We often solve a problem by breaking it into smaller problems
Keep breaking into smaller problems until a problem with a known solution is reached
- This is the base case
Example: Counting down from 10

Counting down from 10

Recursion with Explicit Base Case

public static void countDown(int integer) {
    //Explicit Base Case
    if(integer == 1) { 
        System.out.println(integer);
    } else {
        System.out.println(integer);
        countDown(integer - 1)
    }
}

We state what the stop condition is. Recursion stops when condition is true. integer == 1

Recursion with Implicit Base Case

public static void countDown(int integer) {
    System.out.println(integer);
    //implicit base case
    if(integer > 1) {
        countDown(integer - 1);
    }
}

We state what the continue condition is. The stopping condition is when the continue condition is false.

integer > 1

Tracing the Recursive Method

One method is by Stack Trace

Stack Tracing

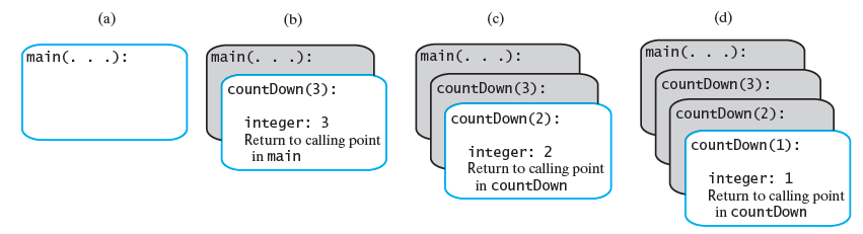
The stack of activation records during the execution of the call countDown(3)

Stack Tracing

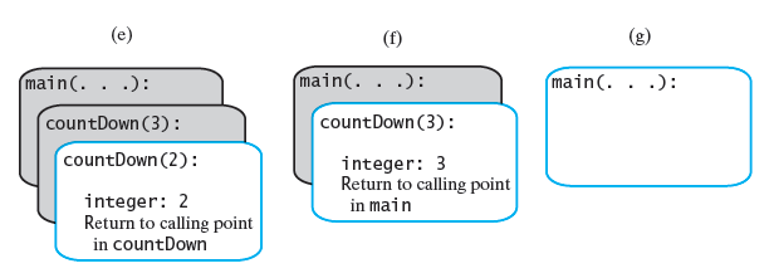
The stack of activation records during the execution of the call countDown(3)

Fundamentals of Recursion

Fundamentals

There must be a base case. Base case can be solved without recursion and is the simplest form of the problem. It is also the termination point where recursion stops.
Every recursive call must progress towards the base case. Otherwise, the base case will never be reached and the recursion will never terminate.
Always assume the recursive call works.
If you have multiple recursive calls in an algorithm, make sure they don’t solve the same instance of a problem more than once.
Any problem that can be solved recursively can also be solved iteratively with extra work.

Question 1

What is wrong with the following recursive method?

public static void countDown(int integer) {
    System.out.println(integer);
    countDown(integer - 1);
}

Answer: There is no base case. The method will never terminate.

Question 2

What is wrong with the following recursive method?

public static void countUp(int integer) {
    if (integer > 0) {
        countUp(integer + 1);
    }
    System.out.println(integer);
}

Answer: The method does not progress twoards the base case for values greater than 0. The base case will never be reached.

Fixing CountUp

How do you fix the countUp method from the previous slide?

public static void countUp(int integer) {
    if (integer > 0) {
        countUp(integer + 1);
    }
    System.out.println(integer);
}

Fixing CountUp

How do you fix the countUp method from the previous slide?

public static void countUp(int integer) {
    if (integer > 0) {
        countUp(integer - 1);
    }
    System.out.println(integer);
}

In the call to countUp we should change the + to a -.

Recursive Methods that Return a Value

Lets compute the sum \(1 + 2 + 3 + ... + (n - 1) + n\)
For any integer \(n > 0\)

public static int sumOf(int n) {
    int sum;

    if(n == 1) {
        sum = 1;
    } else {
        sum = sumOf(n - 1) + n;
    }

    return sum;
}

Tracing SumOf

Tracing the execution of sumOf(3)

Tracing SumOf

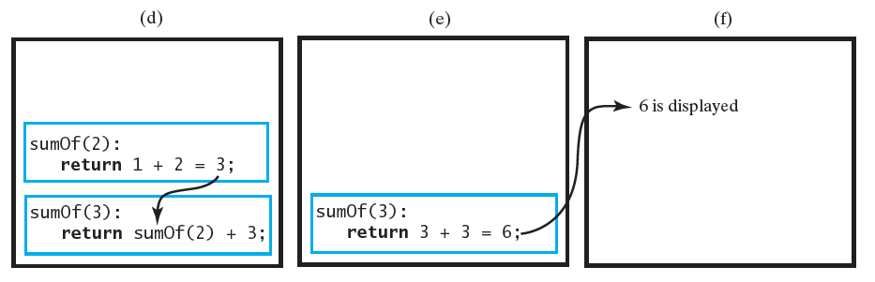
Tracing the execution of sumOf(3)

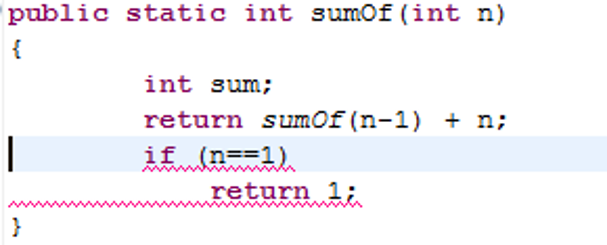
Question

What is wrong with the following sumOf method?

Towers of Hanoi

Simple Solution to Difficult Problem

Recursion can sometimes be a great way to write a solution to a very complicated problem using a very small amount of code
Consider the Towers of Hanoi puzzle

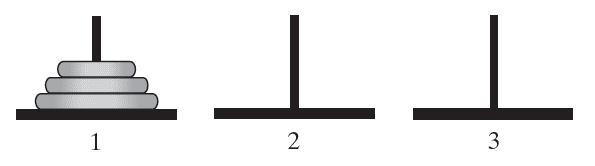
The initial configuration of the Towers of Hanoi for 3 disks

Towers of Hanoi Rules

Move the disks from the first pole to the third pole
1. Move one disk at a time
2. Must only move topmost disk from any pole
3. No disk may rest ontop of a disk smaller than itself

Try yourself!

Solution of 3 Disks

Smallest number of moves is 7

Recursive Solution

The non-recursive solution to this problem is complicated
However, the problem is very easily solved using recursion
To solve for n disks
- Move the top n - 1 disks from first pole to second pole using the third pole temporarily
- The n^th disk is moved to last pole
- Move the top n - 1 disks from the second pole to the third pole using the first pole temporarily

Recursive Solution Illustrated

The smaller problems in a recursive solution for four disks

Recursive Algorithm

Pseudocode

Algorithm solveTowers(numberOfDisks, startPole, tempPole, endPole) {
    if(numberOfDisks > 0) {
        solveTowers(numberOfDisks - 1, startPole, endPole, tempPole)
        Move disk from startPole to endPole
        solveTowers(numberOfDisks - 1, tempPole, startPole, endPole)
    }
}

Java Implementation

public static void solve(int disks, int start, int temp, int end) {
    if(disks > 0) {
        //move n - 1 from start to temp using end as auxiliary
        solve(disks - 1, start, end, temp);
        System.out.println("Move disk " + start + " to " + end);
        //move n - 1 from temp to end using start as auxiliary
        solve(disks - 1, temp, start, end);
    }
}

Problems with Recursion

Biggest issue, not efficient with resources
- Each recursive call creates a new activation record with its own local variables
- Too many recursive calls can cause a StackOverflow error and crash the program
Recursion can result in the same instance of a problem being solved more than once which can reduce performance.

Fibonacci Sequence

Famous recursive sequence
Defined as

\[ \begin{align*} F(0) &= 0 \\ F(1) &= 1 \\ F(n) &= F(n - 1) + F(n - 2) \end{align*} \]

Sequence generated: 0, 1, 1, 2, 3, 5, …, etc.

Recursive Algorithm

Algorithm Fibonacci(n) {
    if n <= 1
        return n
    else
        return Fibonacci(n - 1) + Fibonacci(n - 2)
}

Note the two recursive calls
Example call
- Fibonacci(10) => 55

Tracing Execution

Do not do a stack trace when multiple recursive calls are guaranteed
To trace, use a recursive tree
- First value will be initial value
- Draw branches for each recursive call
  - In the case of Fibonacci, left branch will be the n - 1 call and right branch will be n - 2 call
- Do this for each new branch until you reach a base case

Recursive Tree

Suppose the call is Fibonacci(5)
The value 3 is calculated twice and the value 2 is calculated three times

Recursive Tree

Try Fibonacii(6)!
Can we do better?

Dynamic Programming

It is possible to improve the performance of the recursive Fibonacci while maintaining the elegance of the code
The key is to keep track of values that have already been calculated
This is called dynamic programming
In dynamic programming the solution to each subproblem is only computed once and then stored in a collection and when the subproblem appears again later you just reuse the same solution.

Fibonacci Dynamic Solution

First, let us determine how we want to store the solutions.
Create a table!

n	Fibonacii(n)
0	0
1	1
2	1
3	2
4	3
5	5
6	8
7	13

Notice n can be the values 0 to any positive integer
Looks like an array can be used to keep track of solutions!
This is important because we want a collection that allows for quick retrieval and Arrays don’t get any better!

Fibonacci Dynamic Solution

Lets keep track!

public static int fib(int n) {
    int known[] = new int[n + 1];
    for(int i = 0; i < known.length; i++) {
        known[i] = -1;
    }
    return fib(n, known);
}

private static int fib(int n, int known[]) {
    if(n <= 1) {
        return n;
    }

    if(known[n] != -1) {
        return known[n];
    }

    known[n] = fib(n - 1, known) + fib(n - 2, known);

    return known[n];
}

Notes

Another method was introduced that takes the initial starting value but then calls the recursive method.
- This method is called a guarded method which prevents anyone outside the class from calling the recursive method and passing in bad arguments.
The array was initialized with all -1 values
- This is because by default, the array will contain all 0’s but we need a value that indicates the result is not known
- 0 is a valid result in the sequence given in the previous slides
- So we use -1 instead

Notes continued

There are now two base cases
- The first one determines if we have reached a value less than or equal to 1
- The second one determines if we already know the answer in which case just return the result
In order for this to be efficient, fib(n - 1) must be done FIRST!

Recursive Tree

Now the tree becomes the following

Notice now, we no longer expand already known solutions!

Recursion vs. Iteration

Any problem that can be solved recursively can be solved iteratively. But which is better?
For most problems, an iterative solution is more efficient than a recursive solution
This does not mean that recursion is bad practice!
Recursion sometimes offers elegant solutions to an otherwise extremely difficult problem
More importantly, many algorithms are given as recursive solutions

Time Efficiency of Recursive Algorithms

Below are the steps to take when analyzing the time requirement of a recursive algorithm

Decide on parameter n indicating the input size
Identify the basic operations
Set up a recurrence relation
Solve the recurrence and determine its order of magnitude

Time Efficiency of countDown method

public static void countDown(int n) {
    System.out.println(n);
    if (n > 1) {
        countDown(n - 1);
    }
}

The input size is the size of the integer n.
When n = 1 the statement System.out.println(n) is executed one time for \(O(1)\)
When n > 1 both the println statement and the recursive method call are executed.
- But what is the order of magnitude for the recursive method?

Time Efficiency of countDown method

Let us use \(T(n)\) to represent the time requirement
We get the following relation

\[ \begin{align*} T(1) &= O(1) \\ T(n) &= T(n - 1) + O(1) \end{align*} \]

countDown Recurrence

Expand the recurrence to see behavior
We’ll use \(T(4)\)

Expand to base case \[ \begin{align*} T(4) &= T(3) + O(1) \\ T(3) &= T(2) + O(1) \\ T(2) &= T(1) + O(1) \\ T(1) &= O(1) \end{align*} \]

Go back up substituting previous T(n) solution to right hand side \[ \begin{align*} T(1) &= O(1) \\ T(2) &= O(1) + O(1) = O(2) \\ T(3) &= O(2) + O(1) = O(3) \\ T(4) &= O(3) + O(1) = O(4) \end{align*} \]

countDown Recurrence continued

If we expand for \(T(n)\) we get

\[ \begin{align*} T(n) &= T(n - 1) + O(1) \\ &= T(n - 2) + O(1) + O(1) \\ &= T(n - 3) + O(1) + O(1) + O(1) \\ \dots \\ &= ((n - 1) O(1)) + T(1) \\ &= O(n - 1) + O(1) \\ &= O(n) \end{align*} \]

\(T(1)\) is the base case*

Confirm with Induction

Guess is \(T(n) = O(n)\)
Show base case is true
- \(T(1) = O(1)\) ✓
Show inductive case is true
- \(T(n + 1) = O(n + 1)\)

\[ \begin{align*} T(n + 1) &= T(n) + O(1) \\ &= O(n) + O(1) \\ &= O(n + 1) ✓ \end{align*} \]

Time Requirement of Towers of Hanoi

There were two recursive calls for Towers of Hanoi
\(n\) will represent number of disks
Each call reduced the problem by 1
Recurrence Relation becomes

\[ \begin{align*} T(1) &= O(1) \\ T(n) &= T(n - 1) + T(n - 1) + O(1) \\ &= 2T(n - 1) + O(1) \end{align*} \]

Solving Towers of Hanoi Recurrence

Example of expansion
Reduce to base case

\[ \begin{align*} T(3) &= 2T(3 - 1) + O(1) = 2T(2) + O(1) \\ T(2) &= 2T(2 - 1) + O(1) = 2T(1) + O(1) \\ T(1) &= O(1) \end{align*} \]

Build solution back up from base case

\[ \begin{align*} T(2) &= 2T(1) + O(1) = 2(O(1)) + O(1) = 3O(1) \\ T(3) &= 2T(2) + O(1) = 2(3O(1)) + O(1) = 7O(1) \end{align*} \]

Towers of Hanoi Recurrence

Still not quite seeing a pattern
Create a table!

n	T(n)
1	O(1)
2	3 O(1)
3	7 O(1)
4	15 O(1)
5	31 O(1)

Those multiples are 1, 3, 7, 15, and 31

This leads to O(\(2^n - 1\))

Towers of Hanoi Recurrence

Let us use induction again to check our answer
Our guess: \(T(n) = O(2^n - 1)\)
Base case
- \(T(1) = O(2^n - 1) = O(2^1 - 1) = O(1)\) ✓
Inductive case
- Need to show \(T(n + 1) = O(2^{n + 1} - 1)\)

\[ \begin{align*} T(n + 1) &= 2T((n + 1) - 1) + 1 \\ &= 2T(n) + 1 \\ &= 2(2^n - 1) + 1 \\ &= 2^{n + 1} - 2 + 1 \\ &= 2^{n + 1} - 1 ✓ \end{align*} \]

BigO Final Result

Towers of Hanoi solution is \(O(2^n)\)
That’s a slow algorithm!

BigO Based On Tree

We can get the number of executions by drawing the recursive trees for n = 1, n = 2, n = 3, etc and counting the total number of values in the tree
From that we can deduce the number of calls given n.

Recursive Trees for Towers of Hanoi

n = 1 disk

Only 1 call

n = 2 disks

3 calls

n = 3 disks

7 calls

Recursive Trees for Towers of Hanoi

The trees show that the number of executions becomes

\[ \sum_{i=0}^n{2^i} \]

Because the number of calls made is double the previous number of calls in the tree
This is a well known summation which has \(2^n - 1\) as a closed equation which is what we got above

Fin!

To learn more about recursion, click here