Efficiency of Algorithms
CSC 385 - Data Structures and Algorithms
University of Illinois Springfield
College of Health, Science, and Technology
What is an Algorithm?
- There are ongoing discussions about precise defintion of what an algorithm is
- A basic definition is a series of steps that solves a problem
- This definition is too vague
- Donald Knuth came up with some characterizations that are generally accepted
- Knuth, Donald E. The Art of Programming: Fundamental Algorithms 3rd ed., vol. 1, Addison Wesley, 1997. Chapter 1, Section 1.1.
Finiteness
- An algorithm must always terminate after a finite number of steps
Definiteness
- Each step of the algorithm must be precisely defined
- The actions carried out must be rigorously an unambiguously specified for each use case
Input
- An algorithm has zero or more inputs
- Quantities that are given to it initially before the algorithm begins or dynamically as the algorithm runs
Output
- An algorithm has one or more outputs
- Quantities that have a sepcified relation to the inputs
Effectiveness
- Its operations must all be sufficiently basic that they can in principle be done exactly and in a finite length of time by a person using paper and pencil
What is an algorithm?
- Issues with these characterizations
- What does “defined precisely”, “rigorously and unambiguously specified”, or “sufficiently basic” mean?
- Either way, these characteristics are generally accepted
Algorithm vs. Code
- An algorithm is not code
- Programming languages are a way to express an algorithm for a computer
- Algorithms typically do not provide implementation details
- Pseudocode is another way to express an algorithm that does not contain language specific syntax
rot13-encryption(message, key) {
encrypted = Empty String
for each character in message {
location = (character + key) % alphabet length
encrypted_character = alphabet[location]
encrypted appends encrypted_character
}
return encrypted
}Why Analyze Efficiency?
- Some algorithms will not be able to sovle problems beyond a trivial size in a reasonable amount of time
- Even with the lastest hardware advancements
- Sometimes it is necessary to optimize an algorithm even to gain relatively small improvements in running time
- It makes sense to try to find the most efficient algorithm for solving a problem
- This makes it easier to document and reuse the algorithm and eliminate the need for further improvements
Motivation
- These algorithms solve the same problem but have different efficiencies
sum = 0
for i = 1 to n
sum = sum + isum = 0
for i = 1 to n
{
for j = 1 to i
sum = sum + 1
}sum = n * (n + 1) / 2Three algorithms for computing the sum \(1 + 2 + \dots + n\) for an integer \(n > 0\).
- Even a simple algorithm can be inefficient
Time vs Space
- An algorithm has both time and space requirements called its complexity.
- Time Complexity: The time it takes for the algorithm to execute
- Space Complexity: The memory that the algorithm consumes to execute
- Algorithm’s efficiency is most often measured in terms of its time complexity while space consumption is often overlooked
- This may not cause problems on modern systems with gigabytes of RAM
- Space consumption should still not be ignored especially for systems with limited memory like phones, IOT devices, and embedded devices
- We will refer to running time in this lecture but the same principles apply to space consumption
Measuring Algorithm Efficiency
- The efficiency of an algorithm is measured in terms of its growth rate function
- Growth-rate functions measure how the time/space requirement of the algorithm grows as the number of items it must process increases
- Some functions can be expressed as polynomials while others are exponential or logarithmic
- The linear growth function is one of the easiest to understand
- If an algorithm requires 1 millisecond to process 10 items then it should require 2 milliseconds (twice as much time) to process 20 items (twice as many items)
The Graph
- We often use the variable \(n\) to denote input/problem size
- Graphs of functions are given as the size of inputs (\(n\)) versus the time (\(t\)) of the function
- Time and input size will always be positive integers or 0.
The graph of input size (n) vs time (t)
Quick Note about Time
- When we discuss time complexity we are not talking about seconds, hours, days, etc.
- We are actually talking about number of steps an algorithm takes to complete
- This is important because as hardware gets faster the number of time in seconds may reduce but the number of steps will not
- This is why time is a positive integer or 0 in our measurement of it
- Instead we use…
Asymptotic Notation
- Asymptotic notation is used to describe the behavior of an algorithm
- The three main notated symbols are
- Big-Oh (\(O\)) - order of at most
- Big-Omega (\(\Omega\)) - order of at least
- Theta (\(\Theta\)) - order exactly
- Other notations include little-oh (\(o\)) and little-omega (\(\omega\))
Big O
- The Formal Definition
- \(f(n)\) is order of at most \(O(g(n))\) if there exists a positive constant, \(C\), and a constant, \(N\), such that \(f(n) \leq C * g(n)\) for all \(n \geq \lceil N \rceil\)
- \(f(n)\) is any function
- \(g(n)\) is a class of growth rate functions
- \(C\) is any arbitrary constant
- \(N\) is the input size such that \(g(n)\) starts to overtake \(f(n)\)
- If \(N\) is negative then the right hand side of the inequality will be 0
- \(f(n)\) is order of at most \(O(g(n))\) if there exists a positive constant, \(C\), and a constant, \(N\), such that \(f(n) \leq C * g(n)\) for all \(n \geq \lceil N \rceil\)
- \(g(n)\) is said to be an upper bound of \(f(n)\)
Visual Definition
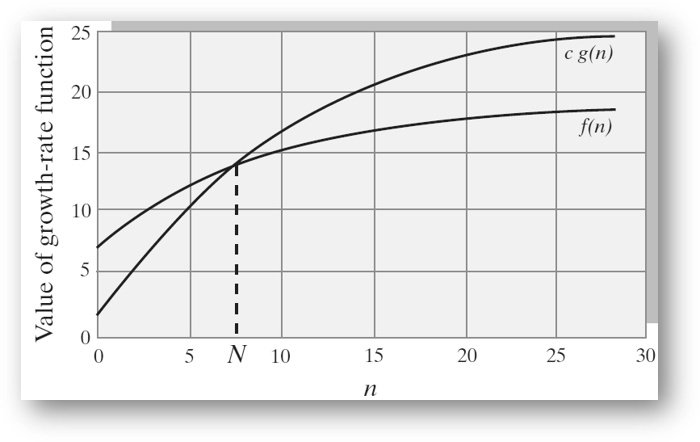
Provided by Frank M. Carrano and Timothy M. Henry
Typical Growth Rate Functions
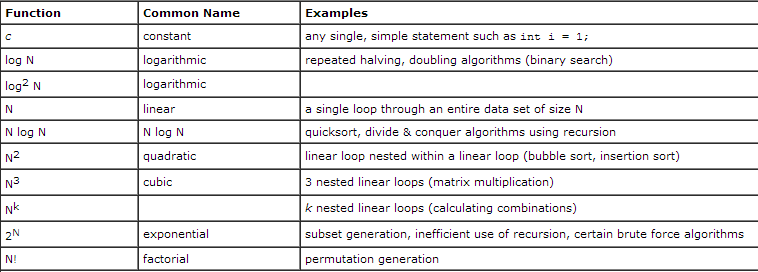
Growth rate functions from most efficient to least efficient. In other words, from slow growth to fast growth
Showing f(n) = O(g(n))
- Suppose we are given the following function
- \(f(n) = 10n + 5\)
- We can show that \(f(n) = O(n)\)
- Start by picking a sufficiently large constant
- \(C = 20\)
- C does not have to be the smallest possible constant. It just has to be large enough to make the BigO inequality true.
Showing f(n) = O(g(n))
- Solve the inequality \(f(n) \leq C * g(n)\) and get a result such that \(n \geq \lceil N \rceil\) where \(n\) is the function variable and \(N\) is a constant.
- \(g(n) = n\) thus \(10n + 5 \leq 20n\)
- Solving this we get \(n \geq \lceil \frac{1}{2} \rceil = n \geq 1\)
- We got a result in the form \(n \geq N\) therefore \(f(n) = O(g(n))\) or \(10n + 5 = O(n)\)
Graph of \(f(n) \leq C * g(n)\)
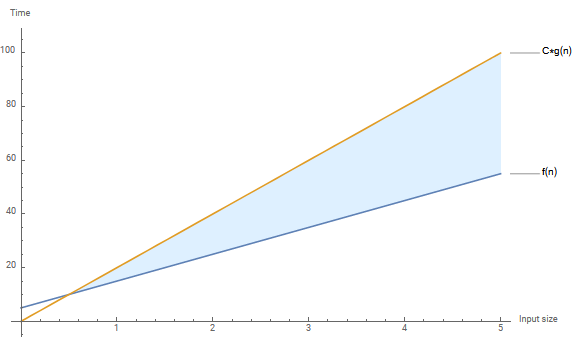
Generated using Mathematica
\(f(n) = 10n + 5\)
\(C\) is the constant 20 and \(g(n) = n\)
Big O Continued
- Given the definition of BigO, this also means that \(f(n) = 10n + 5\) is also \(O(n^2)\)
- Pick constant
- C = 20 (again)
- Solve the inequality \(f(n) \leq C * g(n)\) for all \(n \geq \lceil N \rceil\)
- \(g(n) = n^2\) thus \(10n + 5 \leq 20n^2\)
- \(n \geq \lceil \frac{1}{4} \pm \frac{\sqrt{5}}{-4} \rceil\)
- We only care about positive values so \(n \geq \lceil \frac{1}{4} + \frac{\sqrt{5}}{4} \rceil\)
- This comes out to \(n \geq 1\)
- Pick constant
- Therefore, \(f(n) = O(n^2)\)
Graph of \(f(n) \leq C * g(n)\)
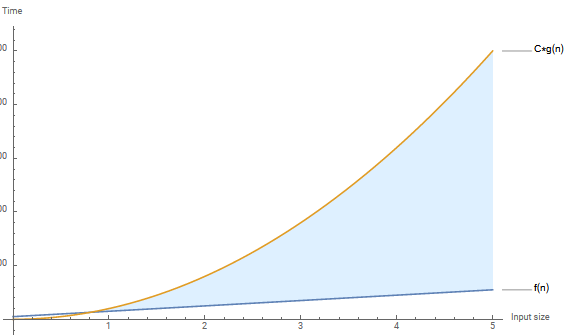
Generated using Mathematica
\(f(n) = 10n + 5\)
\(C=20\) and \(g(n) = n^2\)
Notes on Big O
- We can show that there are many different \(g(n)\) that bounds above \(f(n)\)
- The \(g(n)=n\) for the example function in the previous slide was the tightest upper bound
- \(g(n)\) cannot be a smaller growth rate function otherwise \(f(n)\) would either overtake or never be overtaken by \(g(n)\)
- Big O simply states that a function will grow no faster than \(g(n)\)
- Algorithmically, this means that the program will behave no slower than \(g(n)\)
Picking a Constant
- When deciding a constant, make sure to pick a sufficiently large constant
- For instance, given \(f(n) = 10n + 5\), if we wanted to show \(f(n)=O(n)\) and we pick a constant, \(C=5\), we won’t get the result we want
- \(10n + 5 \leq 5n\) when solved we get \(n \leq -1\)
- This is not in the form \(n \geq -1\) so this is not a good constant
- Nice little trick is to take the sum of the coefficients and pick a non-zero multiple of the sum.
- The coefficients are 10 and 5 so the sum is 15 so pick a multiple of 15 like 30 or 45.
- For instance, given \(f(n) = 10n + 5\), if we wanted to show \(f(n)=O(n)\) and we pick a constant, \(C=5\), we won’t get the result we want
Picking a \(g(n)\)
- When deciding a \(g(n)\), make sure it has an equal or faster growth rate than your \(f(n)\)
- Suppose we have \(f(n) = 10n + 5\) and want to show \(f(n) = O(1)\) (\(O(1)\) is constant time and is represented as \(O(1)\) not \(O(c)\))
- No matter what constant you pick \(f(n)\) will always over take \(g(n) = 1\)
- \(10n + 5 \leq 20g(n) \rightarrow 10n + 5 \leq 20\)
- Solving for \(n\) we get \(n \leq \frac{3}{2}\)
- We do not get an answer in the form \(n \geq N\) which means \(C * g(n)\) never overtakes \(f(n)\) and is overtaken
- This will happen for any constant you pick
Picking a \(g(n)\) continued
- You can do this by picking the highest order and drop its coefficient
- In \(10n + 5\) this highest order is \(10n\). Dropping its coefficient gives \(n\)
- In \(3n^2 + 100n + 50\) the highest order is \(3n^2\). Dropping its coefficient gives \(n^2\)
On \(n \geq \lceil N \rceil\)
- So far, all solutions have had the form \(n \geq \lceil N \rceil\) and this is normal but there is at least one situation where we don’t get this and the function is still in the class of functions
- This occurs when \(f(n)\) is a constant function and \(g(n)\) is also a constant function
- For instance
- \(f(n) = 50\) and we want to show that \(f(n) = O(1)\)
- Pick a sufficiently large C
- \(C = 51\) (we could also pick 50)
- The inequality becomes \(f(n) \leq C * g(n) \rightarrow 50 \leq 51 * 1\)
- This is just true therefore \(f(n) = O(1)\)
- No matter what \(n\) you pick, \(f(n)\) will always be 50 and \(C * g(n)\) will always be above or equal to 50. (as long as \(C \geq 50\) in this case)
Phew
A lot of notes but if you understand BigO then Big\(\Omega\) and \(\Theta\) are easy.
Big\(\Omega\)
- Formal Definition
- \(f(n)\) is order of at least \(g(n)\) if there exists a positive constant \(C\) and positive integer \(N\) such that \(f(n) \geq C * g(n)\) for all \(n \geq \lceil N \rceil\)
- This is BigO except the inequality sign is flipped
- \(g(n)\) is said to be a lower bound of \(f(n)\)
Big\(\Omega\) Continued
- Given \(f(n) = 10n + 5\) let us show that \(f(n) = \Omega(n)\)
- Pick a sufficiently small constant C
- C = 1
- Solve the inequality \(f(n) \geq C * g(n)\)
- \(g(n) = n\)
- \(10n + 5 \geq n\), when solved gives \(n \geq \lceil - \frac{5}{9} \rceil\)
- Since we only care about positive integers then solution becomes \(n \geq 0\)
- Therefore, \(f(n) = \Omega(n)\)
- Pick a sufficiently small constant C
\(10n + 5 \geq n\) Graph
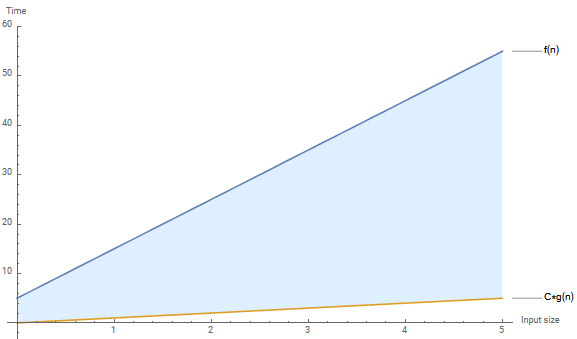
Generated Using Mathematica
Notice that \(f(n)\) overtook \(C * g(n)\) somewher in the negative and stays that way as \(n \rightarrow \infty\)
Big\(\Omega\) Continued
- Just like with BigO we can also show that \(f(n)\) belongs to other classes of functions
- For instance, \(10n + 5 = \Omega(1)\)
- Pick any constant \(C\)
- \(C = 1\)
- Solve inequality \(f(n) \geq C * g(n)\)
- \(10n + 5 \geq 1 * 1 \rightarrow 10n + 5 \geq 1 \rightarrow n \geq -\frac{2}{5}\)
- Again, only dealing with positive integers, so it is still true that when \(n \geq 0\), \(f(n) \geq C * g(n)\) therefore \(f(n) = \Omega(1)\)
- Pick any constant \(C\)
Big\(\Omega\) Continued
- There may only be a limited number of \(g(n)\) that bounds below \(f(n)\)
- When \(f(n) = 10n + 5\) and \(g(n) = n\) then \(g(n)\) was the tightest lower bound
- Any other function with a faster growth rate will overtake \(f(n)\) and not be a Big\(\Omega\) of \(f(n)\)
- For instance, \(10n + 5 \neq \Omega(n^2)\)
\(10n + 5 \geq n^2\) Graph
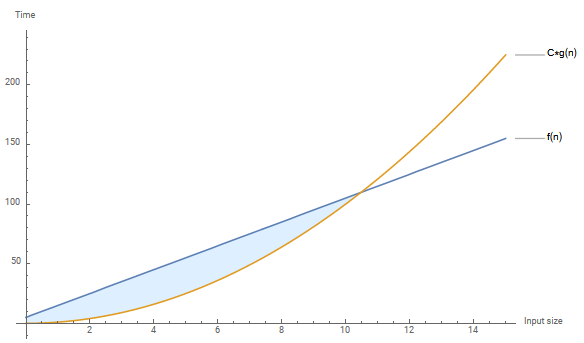
Generated with Mathematica
It is clear to see that \(C * g(n)\) overtakes \(f(n)\)
Theta - \(\Theta\)
- Before moving onto \(\Theta\) you should make sure to understand BigO and Big\(\Omega\)
- Formal definition
- \(f(n)\) is order of \(g(n)\), if and only if, there exists positive integers \(C\) and \(N\) such that \(C * g(n)\) is both lower bound and upper bound on \(f(n)\)
- In other words, if \(f(n) = O(g(n))\) and \(f(n)=\Omega(g(n))\) then \(f(n) = \Theta(g(n))\)
Theta - \(\Theta\) Continued
- Since it was shown that when \(f(n) = 10n + 5\)
- \(f(n) = O(n)\)
- \(f(n) = \Omega(n)\)
- then
- \(f(n) = \Theta(n)\)
- Algorithmically, this means that the algorithm will perform exactly as \(\Theta(n)\)
- Often this is what people in industry mean when talking about efficiency, however, BigO is used as the tightest upper bound of a given algorithm
- BigO is also misued to mean worst-case scenario but we’ll discuss that later
\(10n + 5\) bounded by \(n\)
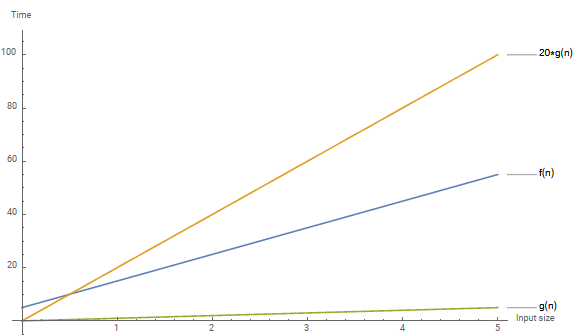
Generated with Matematica
For \(O(n)\), the constant \(C = 20\) was used
For \(\Omega(n)\), the constant \(C = 1\) was used
You can see that \(f(n)\) will stay between \(O(n)\) and \(\Omega(n)\) as \(n \rightarrow \infty\)
Notes on Asymptotic Notation
- It is not correct to put BigO, Big\(\Omega\), or \(\Theta\) on the left of the equals sign
- It is incorrect to say \(O(n) = f(n)\) for instance
- The equals sign as used by asymptotic notation should read as “is a member of” which already has a symbol in set theory
- So more correctly \(f(n) \in O(g(n))\), read \(f(n)\) is a member of \(O(g(n))\) or \(f(n)\) is order at most \(g(n)\)
- However, the equals sign is the more common usage so it will be used throughout the course
More Notes
- BigO is often used in industry when \(\Theta\) is the intent
- For instance, the linear search algorithm is in \(O(n)\)
- As we saw earlier we could equally say it is in \(O(n^2)\) or \(O(n!)\) (one of the worst possible efficiencies in the list).
- But if that were the case then everytime you looped through an array once it would take a very long time
- It should be said that the linear search algorithm is in \(\Theta(n)\) once it has been shown to be bound by \(O(n)\) and \(\Omega(n)\)
- Often, people mean the tightest upper bound when they say BigO.
Best, Worst, and Average
- When discussing an algorithms runtime we often talk about its best, worst, and average case scenarios
- Best case scenario is the set of all inputs that minimizes the algorithms runtime
- Worst case scenario is the set of all inputs that maximizes the algorithms runtime
- Average case scenario is the set of all inputs that require statistical analysis of random inputs. Much harder to reason about average case
- These are not formal definitions but the formal definitions require math beyond the scope of this course
Best, Worst, and Average continued
- Each case can have their own BigO, Big\(\Omega\), and \(\Theta\)
- So when talking about worst case scenarios you can say that a given input will have Big\(\Omega(g(n))\) which means it can do no better than \(g(n)\) for that input
- The running time of some algorithms depends only on size of the data set and not the values of the data
- Example: Finding the smallest element in an array
- The running time of other algorithms may depend on the value of data
- Example: Multiplication of arbitrarily sized values
Best, Worst, Average Examples
- Example of Best Case Scenario
- Searching for an item and it is the first item you look at
- Example of Worst Case Scenario
- Search for an item and it is either the last item you look at or not in the collection
- Example of Average Case Scenario
- Searching for an item and it is between the first item you look at and the last item you look at
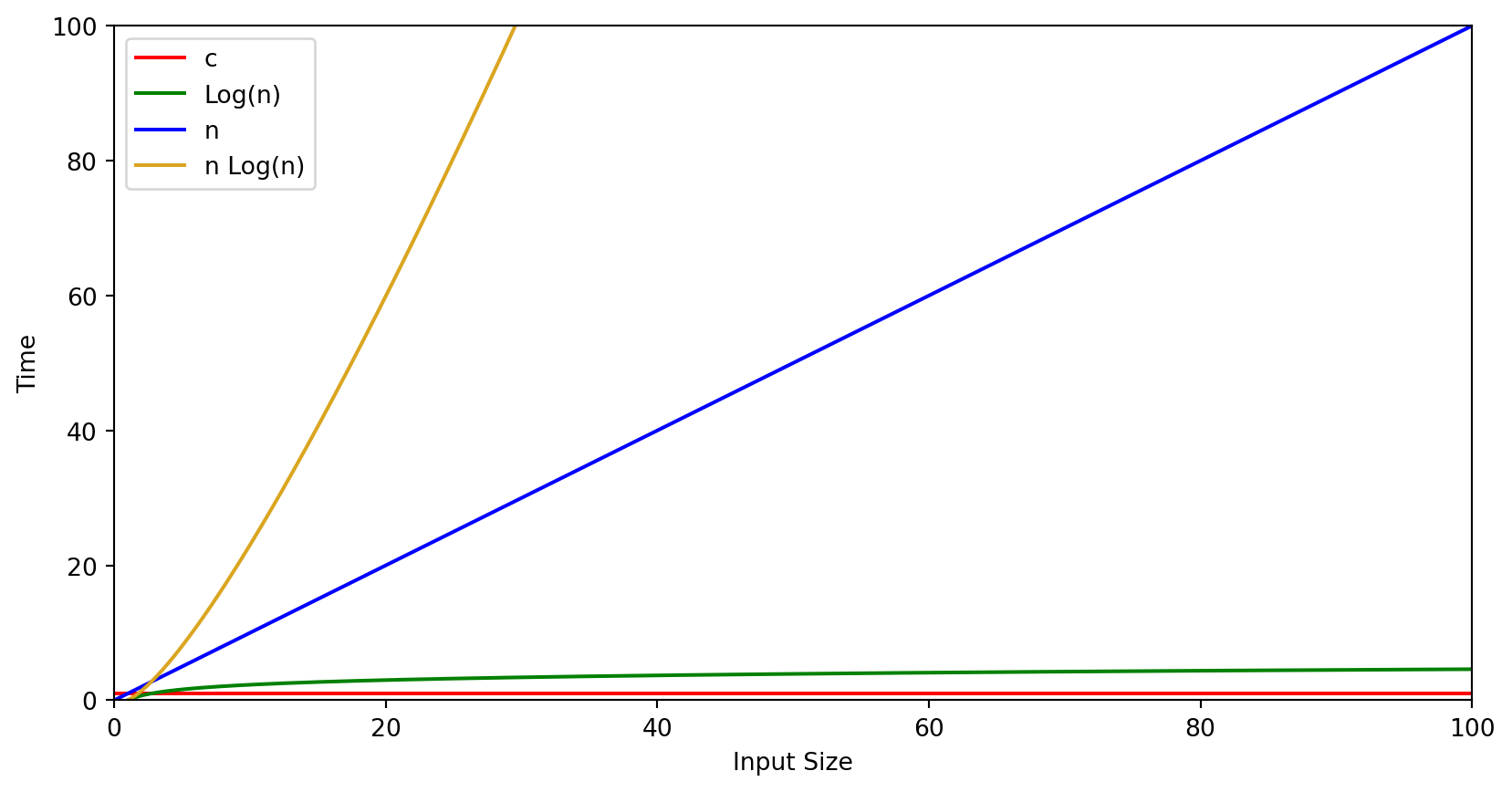
Comparing Growth Rates
Given two algorithms that perform the same task and their BigO notation you can easily dtermine which algorithm should be faster for a given input size by simply substituting the input size in place of \(n\).
We are concerned not with the actual running time but with the rate at which the running time or space consumption increases as the value for \(n\) increases.
- We are interested in the slopes of the growth rate functions and not their values at a particular point
- The less efficient the algorithm, the steeper the slope
Graphs Comparing Growth Rates
Graphs Comparing Growth Rates
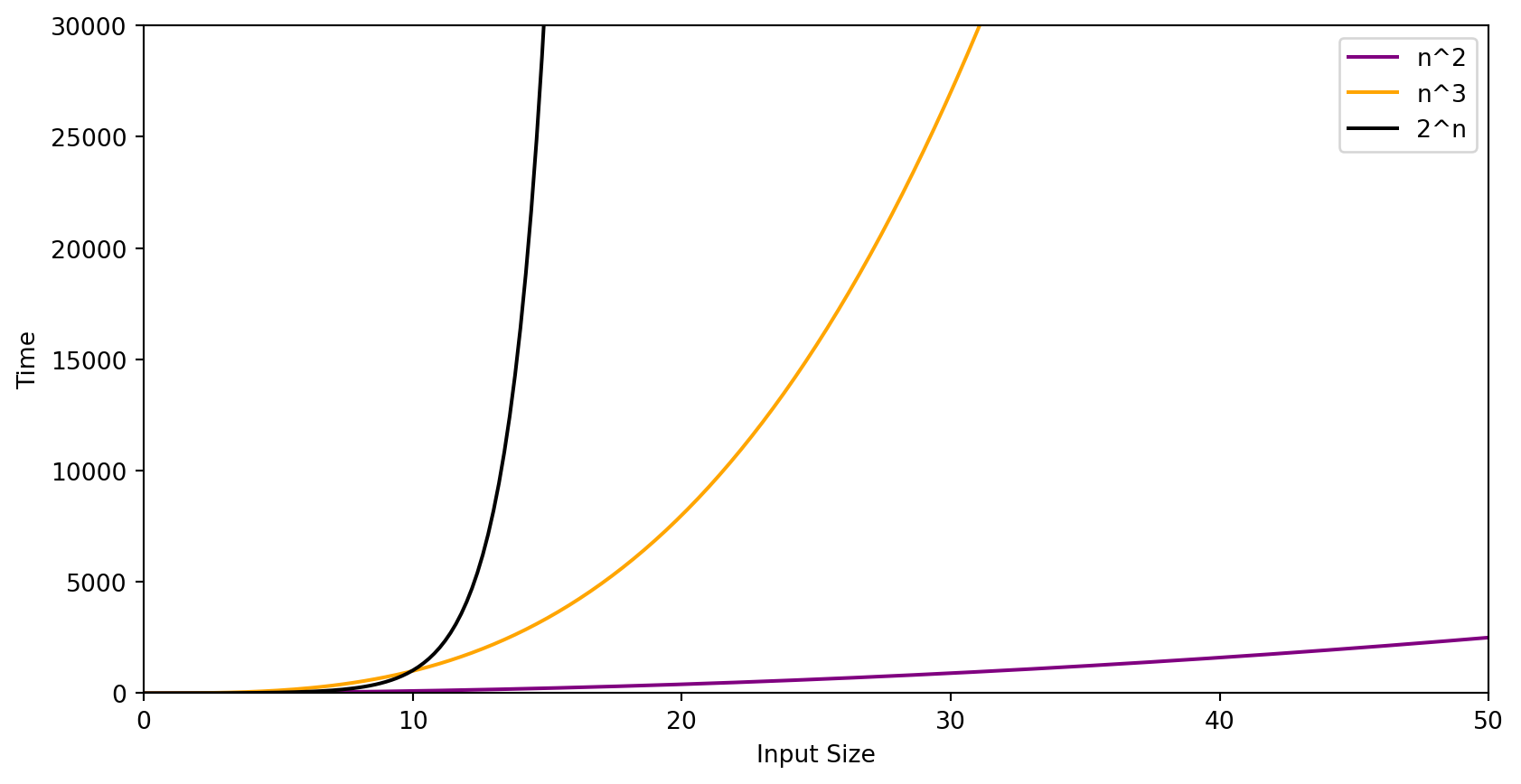
Graphs Comparing Growth Rates
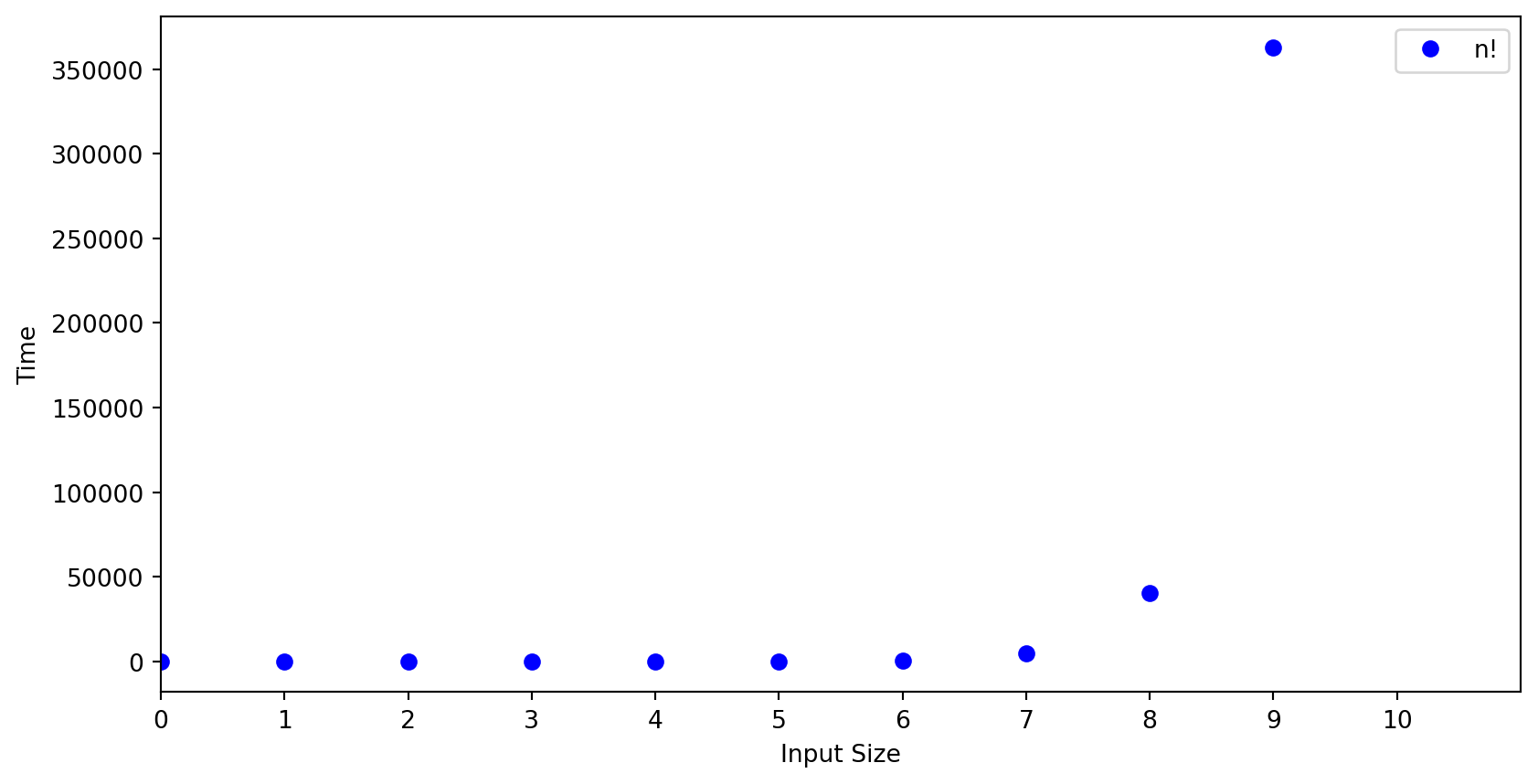
This graph indicates that when \(n = 9\) we are above the 350,000 steps to complete the algorithm. \(9! = 362880\)
Growth Rate Ordering
- From most efficient to least efficient
\(\Theta(1) \le log(log n) \le log n \le log^2 n \le n \le n log n \le n^2 \le n^3 \le 2^n \le n!\)
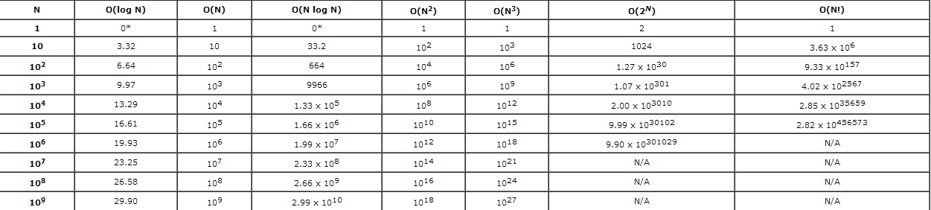
Typical growth-rate functions evaluated at increasing values of n
Precision of BigO
- BigO estimates can be expressed to varying degrees of precision
- \(O(3n^2 + 4n + 7)\) is more precise than \(O(3n^2)\) or \(O(n^2)\) but they are all of quadratic growth
- In general, we are more interested in the general order of the algorithm’s efficiency
- We eliminate all but the highest order term as well as any coefficients of this term
- So the above precisions are typically reduced to \(O(n^2)\)
Precision of BigO Examples
| Precise | Highest order term |
|---|---|
| \(8n^2 + 7\) | \(O(n^2)\) |
| \(8 log n + 5n^3 + 100n^2 + 7\) | \(O(n^3)\) |
| \(5 n log n + n\) | \(O(n log n)\) |
| \(3^n + 6n^4\) | \(O(3^n)\) |
| \(n^{\frac{1}{2}} + 6n^2 log n\) | \(O(n^2 log n)\) |
| \(1000n + \frac{n^2}{log n}\) | \(O(\frac{n^2}{log n})\) |
Determining BigO
- Count the number of times each statement in the algorithm is executed
- Precise BigO value is a sum of all the statement executions
- Counting the total number of statement executions can be tedious and for a complex code it can be very difficult
- Nested loops, recursion, and compound statements can make determining an algorithm’s BigO value quite complicated
- There are tricks we can use to get in the ballpark and determine the highest order which is A-Okay for analyis
Tricks for Computing BigO
- Simple statements such as assignment statements are \(O(1)\)
- A single loop that iterates a variable number of times is \(O(n)\)
- A single loop that iterates anywhere between 1 and n times where the loop’s termination is controlled by the value of some variable is considered \(O(n)\)
- If the loop always iterates a constant number of times, \(C\), such as 10, it is considered \(O(C)\)
- So if \(C = 10\) then we have \(O(10)\)
- For a statement inside a loop, you multiply that statement’s BigO value by the loops BigO value.
- Suppose you have a loop that executes \(O(n)\) times which is in a loop that also executes \(O(n)\) times then you have \(O(n) * O(n)\) or \(O(n^2)\)
Tricks for Computing BigO Continued
- If two loops are consecutive then you just add their BigO values
- For statements that contain calls to other methods you must include the BigO value of the method
- At the end, disregard all but the dominant term, and disregard any coefficient of that term
- The dominant term is the final BigO value
Counting the Statements in a Single Loop
Based on rule 2, the loop iterates N times so it is of \(O(n)\)
Question: What is the actual precise number of total statement executions in this loop?
Sum all statements to get \(1 + n + n + 1 + n = 3n + 2\) which has magnitude \(O(n)\)
Counting Statements in Nested Loop
- Case: Loop index variables are independent
Both loops iterate from 0 to \(N - 1\); i.e., each loop is \(O(N)\). If we apply the rule of multiplying the BigO values of nested loops, we find that overall the nested loops should be \(O(N * N)\), or \(O(N^2)\). That means the statements inside the inner loop are executed \(O(N^2)\) times.
Count Statements in Nested Loop Continued
- Case: Loop index variables are dependent
Nested Loop Continued
Easy way to see what is going on is to write the values for which \(j\) executes. Suppose N = 5.
| i-value/iteration | j-values/iteration | total executions of j-loop |
|---|---|---|
| 0 | 0, 1, 2, 3, 4 | 5 |
| 1 | 1, 2, 3, 4 | 4 |
| 2 | 2, 3, 4 | 3 |
| 3 | 3, 4 | 2 |
| 4 | 4 | 1 |
Nested Loop Continued
To get the total number of statements we have \(5 + 4 + 3 + 2 + 1 = 15\)
Suppose now \(N = 6\). You would see that you would get \(6 + 5 + \dots + 1\) and so on. This is just
\[ \sum_{i=1}^{N} i = \frac{N * (N + 1)}{2} = \frac{N ^ 2 + N}{2} \]
This just becomes \(O(n^2)\) at the end of the day.
More on nested Loops
- Case: Still have dependent index variables
for(int i = 0; i < N; i++) {
for(int j = i; j < N; j++) {
for(int k = j; k < N; k++) {
//statements go here
}
}
}You can take the same approach as the two nested dependent loops but identifying the appropriate function is a little more difficult.
The result is \(\frac{n ^ 3 + 3n^2 + 2n}{6}\) which is just \(O(n^3)\)
Computing the exact number of times that an statement is executed inside nested loops with dependent index variables might be difficult. However, computing the BigO is easy, we just apply rule 3.
Algorithmic Example of Calculating BigO
Maximum Contiguous Subsequence (MCS) Problem
- MCS Problem: Given a sequence of integers \(a_1, a_2, \dots, a_n\) determine the sum of the subsequence of contiguous integers \(a_i, a_{i+1}, a_{i+2}, \dots, a_{k}\) that is the maximum sum for all possible subsequences assumming
- The integers may be positive, negative, or zero
- If all the integers in a subsequence are negative, the sum is zero
- Example: For the sequence -2, -3, 4, -1, 4, 2, 3 the MCS is 4, -1, 4, 2, 3 which has the sum 12. No other subsequence has a sum greater than 12
- We will go over 3 algorithms that solve the MCS problem and compare their efficiencies
Considerations
- We are concerned with worst case scenario
- Therefore, what is the worst case scenario that makes each statement execute?
- In this case, if the entire array contains positive integers
- This may result in strange values but that is because those statements behave based on the above condition
Algorithm 1: Brute-force
- Tries all possible contiguous subsequences
- Is the most straight-forward approach but very inefficient
Algorithm 1 Breakdown
The outermost loop defines the starting position, i, of the subsequence currently being considered. The starting position can be any integer in the sequence, hence the outermost loop goes from the first integer to the last integer.
The middle loop defines the ending position, j, of the subsequence. The ending position can be any position to the right of the starting position
The innermost loop, k, simply goes from the starting position to the ending position and computes the sum of the numbers in the current subsequence.
Analysis of Algorithm 1
public int mcsAlgo1(int nums[]) {
int maxSum = 0; // 1 - time
for(int i = 0; i < nums.length; i++) {
for(int j = i; j < nums.length; j++) {
int currentSum = 0; //N (N + 1) / 2 times
for(int k = i; k <= j; k++) {
currentSum += nums[k]; //(N^3 + 3N^2 + 2N) / 6 times
}
if(currentSum > maxSum) { //N (N + 1) / 2 times
maxSum = currentSum; //N Times
}
}
}
return maxSum; //1 time
}Analysis of Algorithm 1
Sum becomes \[ \begin{gather*} 1 + \frac{N (N + 1)}{2} + \frac{N ^ 3 + 3N^2 + 2N}{6} + \frac{N (N + 1)}{2} + N + 1 \\ = \frac{1}{6} (N^3 + 3N^2 + 2N) + N(N + 1) + N + 2 \\ \end{gather*} \]
This reduces to \(O(N^3)\)
Algorithm 2: Better Brute-Force
- Still tries all possible contiguous subsequences but peforms it in two nested loops instead of 3
- The inner most loop in Algorithm 1 is inefficient and redundant because the sum of some subsequences are computed multiple times
- The loop can be eliminated by maintaining a running sum
Algorithm 2: Better Brute-Force Code
public int mcsAlgo2(int nums[]) {
int maxSum = 0; // 1 time
for(int i = 0; i < nums.length; i++) {
int currentSum = 0; // N times
for(int j = i; j < nums.length; j++) {
currentSum += nums[j]; // N (N + 1) / 2 times
if(currentSum > maxSum) { // N (N + 1) / 2 times
maxSum = currentSum; // N times
}
}
}
return maxSum; // 1 time
}Analysis of Algorithm 2
Sum becomes \[ \begin{gather*} 1 + N + \frac{N * (N + 1)}{2} + \frac{N * (N + 1)}{2} + N + 1 \\ = N * (N + 1) + 2N + 2 \\ = N^2 + N + 2N + 2 \end{gather*} \]
This reduces to \(O(N^2)\)
Algorithm 3: Even Better
- Uses heuristics to avoid looking at every possible subsequence
- Does not consider the subsequences that we know cannot possibly be a contender for the maximum contiguous subsequence
- If the addition produces a negative sum then the maximum contiguous subsequence sum will only be reduced by including the subsequence from i to j
- So we should eliminate this subsequence from consideration by advancing the start of the sequence to j + 1
Algorithm 3 Code
public int mcsAlgo3(int nums[]) {
int maxSum = 0; //1 time
int currentSum = 0; // 1 time
for(int i = 0, j = 0; j < nums.length; j++) {
currentSum += nums[j]; //N times
if(currentSum > maxSum) { //N times
maxSum = currentSum; //N times
} else if(currentSum < 0) { //0 times
i = j + 1; // 0 times
currentSum = 0;// 0 times
}
}
return maxSum;//1 time
}Analysis of Algorithm 3
Sum
\[ \begin{gather*} 1 + 1 + N + N + N \\ = 3N + 2 \end{gather*} \]
Which reduces to \(O(N)\)
Limitations of BigO Analysis
- Problem Size: When the input is small, BigO analysis breaks down
- For small values of \(n\) the term with the highest order may not be dominant
- Example: for \(n < 4\), \(O(10n^2) < O(50n)\)
- Question: Is there a scenerio where the MCS Algorithm 1 is more efficient than MCS Algorithm 3?
- For small values of \(n\) the term with the highest order may not be dominant
Answer
\[ \begin{align*} \frac{1}{6} (N^3 + 3N^2 + 2N) + N(N + 1) + N + 2 &< 3N + 2 \\ \frac{1}{6} (N^3 + 3N^2 + 2N) + N(N + 1) - 2N &< 0 \\ (N^3 + 3N^2 + 2N) + 6N(N + 1) - 12N &< 0 \\ N^3 + 3N^2 + 2N + 6N^2 + 6N - 12N &< 0 \\ N^3 + 9N^2 - 4N &< 0 \\ N (N^2 + 9N + 4) &< 0 \\ \end{align*} \]
This works for values \(N < -9.424\) and \(0 < N < 0.424\) Since we only care about positive integers, and when \(N = 1\), Algorithm 3 is still more efficient, there are no inputs which will make Algorithm 1 more efficient than algorithm 3.
Limitations Continued
- Effect of certain types of operations: The BigO notation does not take into account other types of operations like reading data from a network or the difference between access data on RAM vs a drive.
- The worst case scenario might be very rare: BigO analysis describes how an algorithm will perform when the worst case scenario is encountered but it cannot show if the worst case scenario occurs rarely or not. The performance may be better on average than what a worst case analysis might show.
Practice Questions
Consider two algorithms A and B. Algorithm A requires \(10N^2\) time and algorithm B requires \(1000N\) time. Answer the following.
- Which values of N will algorithm A execute slower than algorithm B?
\[ \begin{align*} 10N^2 &> 1000N \\ 10N^2 - 1000N &> 0 \\ 10N (N - 100) &> 0 \end{align*} \]
This indicates for all \(N > 100\), algorithm A performs worse than algorithm B
Practice Questions Continued
- Which values of N will algorithm A execute faster than algorithm B?
\[ \begin{align*} 10N^2 &< 1000N \\ 10N^2 - 1000N &< 0 \\ 10N (N - 100) &< 0 \end{align*} \]
This indicates for all \(N < 100\), algorithm A performs better than algorithm B
- Which values of N will algorithm A execute the same as algorithm B?
\[ \begin{align*} 10N^2 &= 1000N \\ 10N^2 - 1000N &= 0 \\ 10N (N - 100) &= 0 \end{align*} \]
This indicates for all \(N = 100\), algorithm A performs the same as algorithm B
END
Now take a break. You deserve it!

CSC 385 - Data Structures and Algorithms