Hashing Data Structures

CSC 385 - Data Structures and Algorithms

Brian-Thomas Rogers
broge2@uis.edu

University of Illinois Springfield

College of Health, Science, and Technology

Objectives

Objectives

  • Understand the concept of Dictionary structures and the notion of key-value pairs
  • Understand the difference between a set, map, and table
  • Know what a hashing function does and some of the ways to create a hashing function
  • Understand what collisions are and the four ways they can be resolved

Hashing Data Structures

Basics

  • Take any object and passes it through a function to get some value
  • The value is a positive integer or zero
  • The value is used to map object to a position in an array
  • The two most common hashing structures are dictionaries and sets

Dictionary Types

Dictionary Types

  • A dictionary data structure associates each item with a key

  • This association is commonly referred to as key-value pairs

  • An item is retrieved by searching for its key rather than the item or some index value

  • The two types of hashing data structures we study are

    1. Hashtable
    2. Hashmap

  • Each behave the same way with two distinct differences

    1. hashmaps allow null keys and multiple null values
    2. hashtables are thread safe while hashmaps are not

  • Please note that these particular implementations are for Java’s built-in types and other languages may differ

Hashtables

  • Hashtables are dictionaries in which the key for an item is used to compute the array index where the item resides
  • The function that maps the key to an array index is called the hash function
  • The integer produced by the hash function is called a hash code
  • Ideally the running time to add, retrieve, or remove an item is \(O(1)\)

\[ F(X_{object})_{\text{hash function}} \rightarrow Y_{\text{hash code}} \]

Hashtable Example

  • Suppose we have a hash function we’ll call \(H(key)\)
Key Hash Code Value
“555-0001” \(H(key) = 1\) “100 Elm Road”
“555-1214” \(H(key) = 4\) “150 Main Street”
“555-9998” \(H(key) = 6\) “999 Kanto Drive”

Mapping phone number (key) to array indices which is where the value will be stored

Index Value
0 null
1 “100 Elm Road”
2 null
3 null
4 “150 Main Street”
5 null
6 “999 Kanto Drive”
7 null

Hashtable Definition

public interface HashTable<K, V> { 
  public boolean add(K key, V value);
  public boolean remove(K key);
  public V get(K key);
  public boolean containsKey(K key);
  public boolean containsValue(V value);
  public List<K> keyList();
  public List<V> valueList();
  public void clear();
  public int size();
  public boolean isEmpty();
}
  • Note the two generics K and V
  • K is the type of the key and V is the type of the value
  • The key-value pairs can be of different types

Notes on Hashtables

  • Unlike array-based lists when an item is added or removed it is not necessary to shift other items in a hashtable, gaps are premitted
  • Ideally the array should be the same size as the number of items it contains to ensure efficient use of space
  • A hash function that maps each search key into a unique integer is called a perfect hash function

Note

Perfect hash functions are not possible due to the pigeon hole principle

Computing Hash Codes

Computing Hash Codes

  • Whether for hashtables/maps or hashsets a hashing data structure requires the ability to compute hash codes
  • If keys are integers then they can be used directly
  • If the keys are arbitrary objects (such as a String) then they have to be mapped by the hash function to a non-negative integer as a valid array index

Example Hash Function

  • Suppose we wanted to convert a String to a hash code
  • We observe that characters have a Unicode value that we can use
  • Our first instinct might be to sum these values
public int stringHashFunction(String s) {
    int hashCode = 0;
    for(char c : s.toCharArray()) {
        hashCode += c;
    }
    return hashCode;
}

  • If we call this function using the string “data structures” we get

    • “data structures” = 1566

Example Hash Function Cont.

  • The hash function in the previous slide is not a very good one

  • Suppose we used the same function to map the following string

    • “saturated crust” = 1566

  • We get the same exact hash code for a clearly different String

  • This is known as a hash collision and is something we want to make sure happens infrequently

    • Hash collisions occur when two unique objects produces the same hash code

Example Hash Function Cont.

  • A better approach might be to multiply each character with it’s position in the string starting with 1
public int stringHashFunction(String s) {
    int hashCode = 0;
    int position = 1;
    for(char c : s.toCharArray()) {
        hashCode += c * position;
        position += 1;
    }
    return hashCode;
}

  • Now the string “data structures” and “saturated crust” becomes

    • “data structures” = 12948

    • “saturated crust” = 12445

  • While not perfect, it is harder to accidentally get hash collisions

Map Hash Code to Index

  • What if the hash function produces a hash code that is too large to be a valid index?
  • Suppose the array only has 100 cells but the hash code produced 12948, how do we map this to one of the 100 cells in the array?
  • Simple, just use modulus to get a value between 0 and the length of the array
    • \(12948 \, \% \, 100 = 48\)

Operations for Hash Functions

  • Operations that can be used in a hashing function include:
    • arithmetic operations
    • polynomial operations
    • bit mixing, bit shifting
    • folding (Key is divided into parts which are combined or transformed in various ways)
    • extraction (only a portion of the key is actually used)
    • radix transformation (the key is transformed using another number base)
    • mod functions (used to ensure the hash code is within a valid range of indexes)

Properties of a Good Hash Function

  • Things to consider when creating or choosing a hash function
    1. It should not generate any negative values
    2. It should be able to cover every cell in an array (no cells should remain forever empty)
    3. It should generate evenly distributed hash codes (minimal collisions)
    4. It should be fast to compute

Terminology

Terminology

  • Load Factor: the fraction of the hash table that is full
    • If the size of the hash table is 20 and it only has 14 entries you can say its load factor is \(14 / 20 = 0.7\) or 70%.
  • Threshold: determines when to resize the array before being completely filled
    • If the threshold is set to 0.75, this means when the load factor is 0.75 or more then the array has to be resized
  • When the array is resized due to the load factor reaching the threshold, each item must be rehashed and placed back in the array in a new location
    • Rehashing is \(O(n*h)\) where \(h\) is the process of hashing the object

Collisions

Collisions

  • A hash function is not guaranteed to generate a unique index for every key
  • Two key values might be mapped to the same array index
  • This is known as a collision
G F(X) F(X) Hashcode Hashcode F(X)->Hashcode same Object1 Object1 Object1->F(X) Object2 Object2 Object2->F(X)

Assuming \(Object1 \neq Object2\) and F(X) is a hash function

Collision Resolution

  • There are two main ways to resolve collisions
    • Use another location in the array (open addressing)
      • Linear Probing
      • Quadratic Probing
      • Double Hashing
    • Restructure the hash table so that each array location can represent more than one value
      • Separate Chaining (Buckets)

Linear Probing

  • Array is scanned sequentially from the initial location until an empty cell is found
    • Collision at a[k]
    • Check for open cell at a[k + 1], a[k + 2], etc.
    • The scanning process should be capable of wrapping around to the beginning of the array when the end of the array is reached
  • Linear probing ensures the success of the add operation as long as the hash table is not full
  • If linear probing is used to resolve collision then it will have to package the key with its value in the array cell to make it possible to retrieve an entry with its key

Linear Probe Example

The cells each contain both the key and value

Linear Probe Question

  • Assuming that linear probing is used, when retrieving an item, what happens if the item is not in the hashtable?
  • Answer: The probe will encounter a cell with a null value indicating an unsuccessfull search
    • This can be a problem, however, when removing

Removals and Null

  • Problem
    • Suppose there are items that are contiguous in the array between a[k] and a[k + 3]
    • The elements at a[k] and a[k + 3] have a hash collision
    • The elements at a[k + 1] and a[k + 2] are removed by setting their corresponding locations to null

h(555-2072) can’t be reached

Removals and Null Cont.

  • The issue is now linear probing can’t find the element at a[k + 3] due to the condition that a null was encountered at a[k + 1]
  • Removal must be marked differently
    • Instead of null, use a value to show the cell is available but location’s entry was removed
    • So every array cell can have three states: null, occupied, or available
  • Location can be reused for add

Disadvantages of Linear Probing

  • If the array is heavily populated, finding the first empty cell takes longer
  • Primary Clustering
    • Occurs if the hash function frequently produces the same hash code
      • Items tend to be clustered around the same array index
      • Items are not evenly distributed
      • Running time will be dominated by collision resolution
      • Performance decreases

Quadratic Probing

  • Avoid primary clustering by changing the sequence
  • Instead of linearly examining consecutive cells
    • Go to k + 1, then k + 4, then k + 9
    • In general, go to \(k + j^2\) for \(j = 1, 2, 3, \dots\)

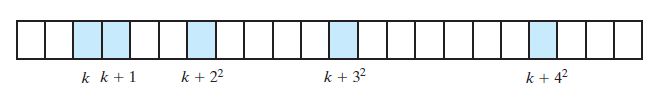
Practice Question

  • Suppose we have the following table of Objects and their hash values and we want to insert them into an array of size 13
Item Hash Code Array Index
Dallas Cowboys 137 137 % 13 = 7
New York Giants 358 358 % 13 = 7
Miami Dolphins 564 564 % 13 = 5
Arizona Cardinals 674 674 % 13 = 11
Chicago Bears 540 540 % 13 = 7
Detroit Lions 752 752 % 13 = 11
Green Bay Packers 748 748 % 13 = 7

Answer

Index Array
0 null
1 null
2 null
3 Chicago Bears
4 null
5 Miami Dolphins
6 null
7 Dallas Cowboys
8 New York Giants
9 null
10 Green Bay Packers
11 Arizona Cardinals
12 Detroit Lions

Quadratic Probing Cont.

  • Quadratic probing avoids the problem of primary clustering by allowing gaps between the probing sequence
  • Some secondary clustering occurs
    • The same alternative cells are examined when a collision occurs at a given array index
    • Secondary clustering is generally not as extensive as primary clustering

Double Hashing

  • Use a second hash function to compute increments in key-dependent way
    • \(H(key) = k\), Collision at a[k]?
    • Use second hash function \(H_2(key)\) and examine \(k + H_2(key)\), \(k + 2 * H_2(key)\), \(k + 3 * H_2(key)\), etc.
  • Second hash function should reach entire table
  • Avoids both primary and secondary clustering
  • Drawback: cost of applying second hash function

Example

  • \(H_1(key) = key \mod 7\)
  • \(H_2(key) = 5 - key \mod 5\)

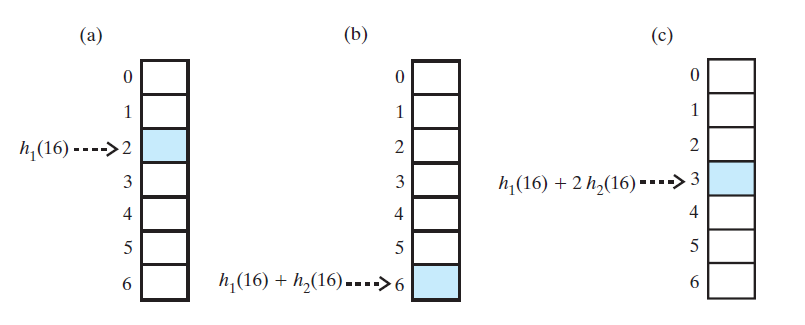
The first three locations in a probe sequence generated by double hashing for the search key 16

Separate Chaining

  • The idea is simple: each cell is a linked list
  • This is called a bucket (remember radix sort? Same principle)
  • The items that hash to the same cell are stored in the linked list

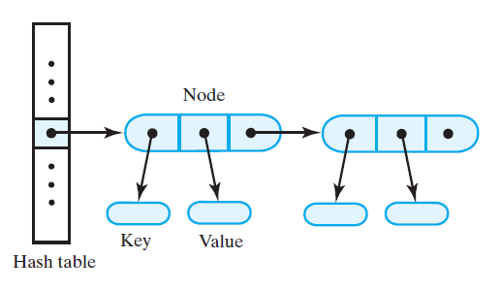
Separate Chaining Note

  • Even if the items are inserted into a linked list they still count towards the load factor
  • This means that an array of size 10 that has 5 items spread to different cells or all in the same cell (same bucket) still has a load factor of 50%
  • When the load factor reaches the threshold the resize could potentially spread the items out more evenly

Collisions and Running Time

  • Ideally the add, remove, and retrieval operations have a constant time \(O(1)\)
  • Collision, however, can affect running time
    • If collision happens infrequently or only a small amount of probing is required
      • Cost of collision handling can be amortized
      • The resulting running time can be considered \(O(1)\)

HashTable Implementation

HashTable Implementation

  • When considering to implement your own hashtable there is an initial problem
    • How do you come up with a hash function that can handle any type of object?
  • You don’t!
    • Java’s Object class has a method called hashCode() that should be overridden by the creator of a class
    • In the implementation of any Hashing data structure, you should use this method
    • Other languages may differ

Java Documentation for hashCode() method

Java Docs for HashTable and HashMap

Example of Using a HashMap

import java.util.HashMap;
import java.util.Scanner;

public class Example {
  public static void main(String args[]) {
    Scanner userin = new Scanner(System.in);
    String line = userin.nextLine().trim();
    userin.close();

    HashMap<Character, Integer> frequency = new HashMap<>();

    for(char c : line.toCharArray()) {
      if(frequency.containsKey(c)) {
        int currentCount = frequency.get(c);
        currentCount += 1;
        frequency.replace(c, currentCount);
      } else {
        frequency.put(c, 1);
      }
    }

    System.out.println(frequency);
  }
}
  • Displays the character frequency of a provided text

Refactored

import java.util.HashMap;
import java.util.Scanner;

public class Example {
  public static void main(String args[]) {
    Scanner userin = new Scanner(System.in);
    String line = userin.nextLine().trim();
    userin.close();

    HashMap<Character, Integer> frequency = new HashMap<>();

    for(char c : line.toCharArray()) {
      int currentCount = frequency.getOrDefault(c, 0);
      currentCount += 1;
      frequency.put(c, currentCount);
    }

    System.out.println(frequency);
  }
}
  • The use of the method getOrDefault allows us to either get the value using the key c if it exists else return 0.

Hash Sets

Hash Sets

  • Is a collection that contains no duplicate items
  • Unlike maps, items are NOT associated with keys
  • Often used in database queries to avoid duplicate items
  • The JDK library provides one hashset type

Hash Set Implementation

  • Easier than a HashMap/Table
  • You only need a single generic for the items to store
  • You still utilize a hash function
  • You still need to deal with collisions
  • Don’t allow duplicates!

End

CSC 385 - Data Structures and Algorithms