AVL Trees

CSC 385 - Data Structures and Algorithms

Brian-Thomas Rogers

broge2@uis.edu

University of Illinois Springfield

College of Health, Science, and Technology

Contents

• Objectives
• AVL Tree Basics
• Rotations
• AVL Tree Implementation
• Practice Questions
• End

Objectives

Objectives

• Know what balance means in the context of binary search trees
• Understand the balancing rules for an AVL Trees
• Know the algorithms for performing the four different rotations
• Know that the worst-case running times for an unbalanced tree are \(O(n)\) but \(O(log n)\) for a properly balanced tree

AVL Tree Basics

AVL Tree Basics

• Created by Adelson-Velsky and Landis
• AVL Trees are balanced Binary Search Trees using the following property
  • For any given node in an AVL tree, the heights of the node’s left and right subtrees may differ by at most 1
• If the ballance of a binary tree is lost after adding or removing items the AVL Tree rearranges the nodes by rotation to keep maintain balance

Rotations

Imbalance Cases

• There are 4 cases when a node X becomes imbalanced
  • Case 1: Imbalance is in the left subtree of X’s left child
  • Case 2: Imbalance is in the right subtree of X’s right child
  • Case 3: Imbalance is in the right subtree of X’s left child
  • Case 4: Imbalance is in the left subtree of X’s right child

Imbalance Case 1

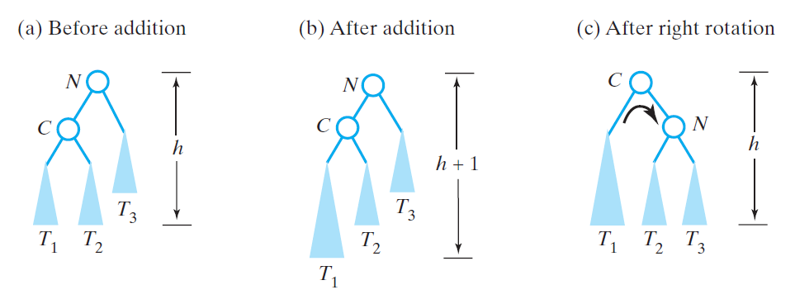
The imbalance is fixed with a right rotation

• Algorithm for right rotation about N
  1. C = N.left
  2. N.left = C.right
  3. C.right = N

Imbalance Case 1 Initial Tree

Imbalance Case 1 Rotation

• Add node 1 to the tree
• The imbalance is detected by the root node 10
  • Left subtree height is 4 while right subtree height is 2
  • The imbalance is in 10’s left child’s left subtree.
• A right rotation happens about the root

Imbalance Case 1 After Rotation

• Height of both left and right subtrees are now 3
• The tree is balanced

Imbalance Case 2

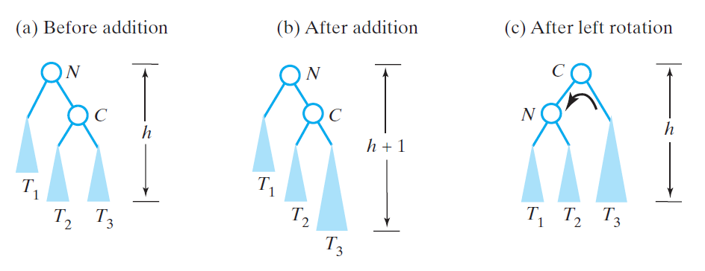
The fix for this case is by using a left rotation

• Algorithm for left rotation about node N
  1. C = N.right
  2. N.right = C.left
  3. C.left = N

Imbalance Case 2 Initial Tree

Imbalance Case 2 Rotation

• Add node 40 to the tree
• The imbalance is detected by the root node 10
  • Left subtree has height 2 while right subtree has height 4
  • The imbalance is in 10’s right child’s right subtree
• A left rotation happens about the root

Imbalance Case 2 After Rotation

• The height of the left and right subtree at the root is 3.

Imbalance Case 3

• The imbalance of case 3 is fixed by doing double rotations
  • First, perform a left rotation on the imbalanced child
  • Then, perform a right rotation on the parent

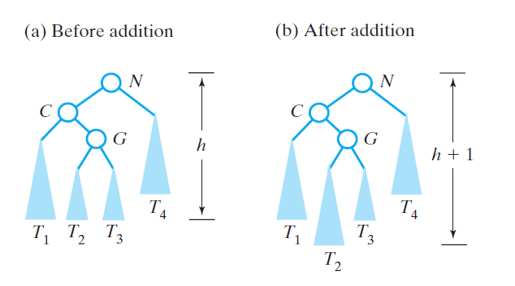
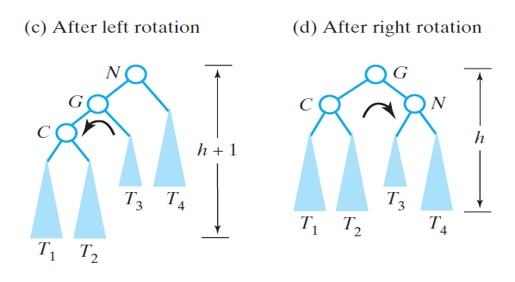
Imbalance Case 3 Initial Tree

Imbalance Case 3 First Rotation

• Tree becomes imbalanced when 10 is added
• Imbalance occurs in 12’s left child’s right subtree
  • Left Rotation occurs on the left child first
  • Result on next slide

Imbalance Case 3 Second Rotation

• Tree is still imbalanced so we do a right rotation about 12 now

Imbalance Case 3 After Rotations

• After the last rotation the tree becomes balanced

Imbalance Case 4

• The imbalance of case 4 is fixed by doing double rotations
  • First, perform a right rotation on the imbalanced child
  • Then, perform a left rotation on the parent

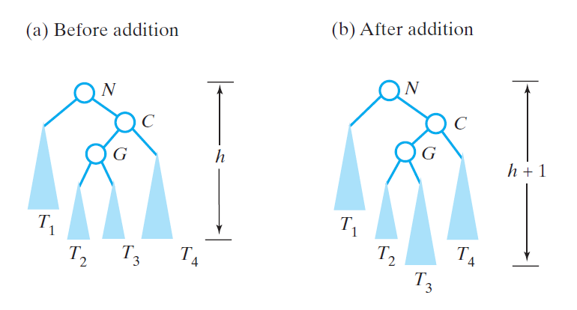
Imbalance Case 4 Initial Tree

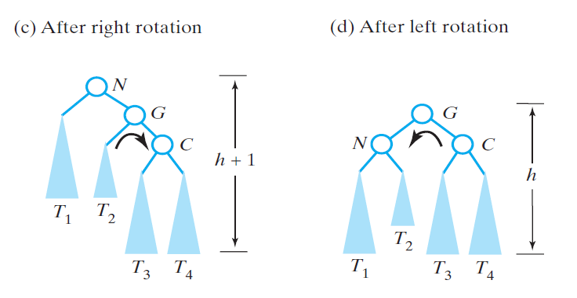
Imbalance Case 4 Right Rotation

• Tree imbalanced after adding 18
  • Perform right rotation about 20
  • Result on next page

Imbalance Case 4 Left Rotation

• Tree is stil imbalanced so now we do a left rotation

Imbalance Case 4 After Rotations

• Tree is balanced after performing both rotations

Notes

• The examples have the rotation in the root of the tree but this is not always the case
• Here is an example where a rotation happens but not on root

• Here, the imbalance occurs in 20’s right child’s right subtree after adding 40
• This requires a left rotation about 20
• Root will then have a balance of left height 1, right height 2 after the rotation

AVL Tree Implementation

AVL Tree Implementation

• Similar to the binary search tree with the following additions
  • The TreeNode class now has additional properties to keep track of the height of the subtrees
  • There are 2 additional methods for the rotations, a method to rebalance, and utility methods to fix the height of a node and a method to calculate the balance of a subtree
  • The add and remove must include the balance correction mechanism
  • The add and remove becomes a two-pass algorithm
    • First pass either adds or removes a node by traversing down the tree
    • Second pass corrects imbalances by backtracking the path taken and fixing the height property of each node and correcting any imbalances that occur

Practice Questions

Question 1

• What rotation/rotations need to be performed on the following tree after John is added?

Answer 1

• Working backwards from John we see Ellie is balanced with left height 0 and right height 1 but Tania is imbalanced with left height 2 and right height 0.
• Where does the imbalance occur?
  • Tania’s left child’s right subtree
  • This is case 3 so a left rotation then right rotation

Perform Left Rotation about Ellie

Rotate right about Tania

Answer 1 Complete

Practice Question 2

• What rotation/rotations need to be performed to balance the following Tree after adding Nat?

Answer 2

• Working backwards from Nat we see that Matt is balanced, Oscar is balanced, but Frank is not
• Where does the imbalance occur?
  • Frank’s right child’s left subtree
  • This is case 4 so a right rotation and then a left rotation

Perform Left Rotation about Oscar

Rotate right about Frank

Answer 2 Complete

End